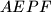
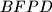
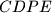
Neka je točka u unutrašnjosti trokuta . Neka su , i nožišta okomica iz točke na pravce , i redom. Ako su četverokuti , i tangencijalni, dokaži da je središte trokutu upisane kružnice.
%V0
Neka je $P$ točka u unutrašnjosti trokuta $ABC$. Neka su $D$, $E$ i $F$ nožišta okomica iz točke $P$ na pravce $BC$, $CA$ i $AB$ redom. Ako su četverokuti $AEPF$, $BFPD$ i $CDPE$ tangencijalni, dokaži da je $P$ središte trokutu $ABC$ upisane kružnice.
Školjka 
točka u unutrašnjosti trokuta 
. Neka su 
, 
i 
nožišta okomica iz točke 
, 
i 
redom. Ako su četverokuti 
, 
i 
tangencijalni, dokaži da je