Županijsko natjecanje 1996 SŠ3 3
Dodao/la:
arhiva1. travnja 2012. Duljine stranica trokuta su
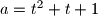
,
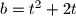
i
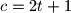
, gdje je

pozitivan realan broj.
(a) Poredajte te duljine po veličini.
(b) Dokažite da je
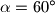
.
(c) Izračunajte polumjere

i

opisane i upisane kružnice tog trokuta i nađite najmanji mogući omjer
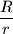
.
(d) Nađite vrijednosti

za koje je trokut pravokutan.
%V0
Duljine stranica trokuta su $a=t^2+t+1$, $b=t^2+2t$ i $c=2t+1$, gdje je $t$ pozitivan realan broj.
(a) Poredajte te duljine po veličini.
(b) Dokažite da je $\alpha=60^{\circ }$.
(c) Izračunajte polumjere $R$ i $r$ opisane i upisane kružnice tog trokuta i nađite najmanji mogući omjer $\dfrac{R}{r}$.
(d) Nađite vrijednosti $t$ za koje je trokut pravokutan.
Izvor: Županijsko natjecanje iz matematike 1996