Županijsko natjecanje 2001 SŠ3 2
Dodao/la:
arhiva1. travnja 2012. Točka
nalazi se unutar trokuta
tako da je
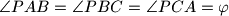
. Ako su
,
i
kutovi trokuta, dokažite da je
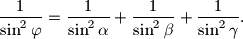
%V0
Točka $P$ nalazi se unutar trokuta $ABC$ tako da je $\angle PAB=\angle PBC=\angle PCA=\varphi$. Ako su $\alpha $, $\beta $ i $\gamma $ kutovi trokuta, dokažite da je $$
\dfrac{1}{\sin ^2\varphi }=\dfrac{1}{\sin ^2\alpha }+
\dfrac{1}{\sin ^2\beta }+\dfrac{1}{\sin ^2\gamma }.
$$
Izvor: Županijsko natjecanje iz matematike 2001
Školjka 
