Županijsko natjecanje 2004 SŠ3 3
Dodao/la:
arhiva1. travnja 2012. Neka je

pravokutni trokut s katetama duljina

i

i hipotenuzom duljine

, a
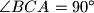
. Neka je

tom trokutu opisana kružnica,

kružnica koja dodiruje hipotenuzu, visinu

i luk
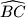
kružnice

; te

kružnica koja dodiruje hipotenuzu, visinu

i luk
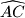
kružnice

. Ako su
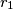
i
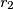
polumjeri kružnica

i

dokažite da je
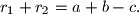
%V0
Neka je $ABC$ pravokutni trokut s katetama duljina $a$ i $b$ i hipotenuzom duljine $c$, a $\angle BCA=90^\circ$. Neka je $k$ tom trokutu opisana kružnica, $k_1$ kružnica koja dodiruje hipotenuzu, visinu $\overline{CD}$ i luk $\widehat{BC}$ kružnice $k$; te $k_2$ kružnica koja dodiruje hipotenuzu, visinu $\overline{CD}$ i luk $\widehat{AC}$ kružnice $k$. Ako su $r_1$ i $r_2$ polumjeri kružnica $k_1$ i $k_2$ dokažite da je $$
r_1+r_2=a+b-c.
$$
Izvor: Županijsko natjecanje iz matematike 2004