Županijsko natjecanje 2009 SŠ3 5
Dodao/la:
arhiva1. travnja 2012. Kvadratna tablica
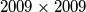
popunjena je brojevima
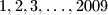
tako da se u svakom retku i svakom stupcu pojavljuje svaki od tih brojeva. Ako je tablica simetrična u odnosu na jednu dijagonalu, onda se i na toj dijagonali pojavljuju svi brojevi
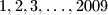
. Dokaži!
%V0
Kvadratna tablica $2009 \times 2009$ popunjena je brojevima $1, 2, 3, \dots, 2009$ tako da se u svakom retku i svakom stupcu pojavljuje svaki od tih brojeva. Ako je tablica simetrična u odnosu na jednu dijagonalu, onda se i na toj dijagonali pojavljuju svi brojevi $1, 2, 3, \dots, 2009$. Dokaži!
Izvor: Županijsko natjecanje iz matematike 2009