Županijsko natjecanje 2010 SŠ3 5
Dodao/la:
arhiva1. travnja 2012. Neka je

prirodni broj,
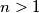
. Kvadratići ploče
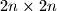
obojani su plavom ili crvenom bojom tako da za svaka dva retka postoji točno

stupaca sa svojstvom da su dva kvadratića na presjeku tog stupca i promatranih dvaju redaka obojana istom bojom. Dokaži da broj

mora biti paran.
%V0
Neka je $n$ prirodni broj, $n>1$. Kvadratići ploče $2n \times 2n$ obojani su plavom ili crvenom bojom tako da za svaka dva retka postoji točno $n$ stupaca sa svojstvom da su dva kvadratića na presjeku tog stupca i promatranih dvaju redaka obojana istom bojom. Dokaži da broj $n$ mora biti paran.
Izvor: Županijsko natjecanje iz matematike 2010