Županijsko natjecanje 2012 SŠ3 2
Dodao/la:
arhiva1. travnja 2012. Kugli polumjera

opisan je tetraedar (trostrana piramida). Ako su duljine visina tog tetraedra
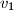
,
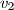
,
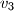
i
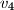
, dokaži da vrijedi
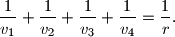
%V0
Kugli polumjera $r$ opisan je tetraedar (trostrana piramida). Ako su duljine visina tog tetraedra $v_1$, $v_2$, $v_3$ i $v_4$, dokaži da vrijedi $$\frac 1{v_1}+\frac 1{v_2}+\frac 1{v_3}+\frac 1{v_4}=\frac 1r.$$
Izvor: Županijsko natjecanje iz matematike 2012