Županijsko natjecanje 2012 SŠ3 3
Dodao/la:
arhiva1. travnja 2012. Dokaži da ne postoji racionalni broj

takav da je
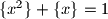
.
Odredi barem jedan realni broj

koji zadovoljava tu jednakost.
Oznaka
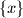
predstavlja razlomljeni dio od

, tj.
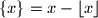
pri čemu je
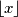
najveći cijeli broj koji nije veći od

. Npr.
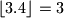
,
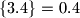
.
%V0
Dokaži da ne postoji racionalni broj $x$ takav da je $\{x^2\}+\{x\}=1$.
Odredi barem jedan realni broj $x$ koji zadovoljava tu jednakost.
Oznaka $\{x\}$ predstavlja razlomljeni dio od $x$, tj. $\{x\}=x-\lfloor x\rfloor$ pri čemu je $\lfloor x\rfloor$ najveći cijeli broj koji nije veći od $x$. Npr. $\lfloor 3.4\rfloor = 3$, $\{3.4\}=0.4$.
Izvor: Županijsko natjecanje iz matematike 2012