Zadani su realni brojevi

. Odredite sve mogućnosti izbora brojeva

,

,

,

za koje je
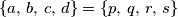
, a vrijednost izraza
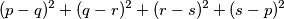
je najmanja.
%V0
Zadani su realni brojevi $a<b<c<d$. Odredite sve mogućnosti izbora brojeva $p$, $q$, $r$, $s$ za koje je $\{a,\,b,\,c,\,d\}=\{p,\,q,\,r,\,s\}$, a vrijednost izraza $$(p-q)^2+(q-r)^2+(r-s)^2+(s-p)^2$$ je najmanja.