Izborno natjecanje 2002 - Zadatak 2
Kvaliteta:
Avg: 0,0Težina:
Avg: 4,0Neka je  tangencijalni četverokut. Neka se pravci
tangencijalni četverokut. Neka se pravci  i
i 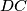 sijeku u točki
sijeku u točki  , a pravci
, a pravci 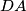 i
i  u točki
u točki  pri čemu točka
pri čemu točka  leži između
leži između  i
i  ;
;  između
između  i
i  ;
;  između
između  i
i  te
te  između
između  i
i  . Neka su
. Neka su 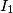 ,
, 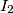 i
i 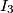 redom središta kružnica upisanih trokutima
redom središta kružnica upisanih trokutima 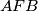 ,
, 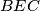 i
i  . Pravac
. Pravac 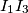 siječe pravce
siječe pravce 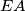 i
i 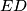 u točkama
u točkama  i
i  redom, a pravac
redom, a pravac 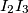 pravce
pravce 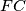 i
i 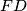 u točkama
u točkama  i
i  redom.
redom.
Dokažite da je 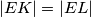 ako i samo ako je
ako i samo ako je 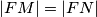 .
.
Izvor: Izborno natjecanje 2002.
 Školjka
Školjka 
