Školjka

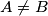Neka je $B$ točka na kružnici $k_1$, $A \neq B$ točka na tangenti te kružnice u točki $B$ i $C$ točka koja ne leži na $k_1$ takva da dužina $\overline{AC}$ siječe $k_1$ u dvije različite točke. Neka je $k_2$ kružnica koja dodiruje pravac $AC$ u točki $C$ i kružnicu $k_1$ u točki $D$, a leži u poluravnini određenoj pravcem $AC$ u kojoj se ne nalazi točka $B$. Dokažite da središte kružnice opisane trokutu 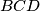$BCD$ leži na opisanoj kružnici trokuta $ABC$.