Izborno natjecanje 2007 - Izborni test za MEMO - Zadatak 2
Dodao/la:
arhiva18. listopada 2023. Dokažite da među brojevima 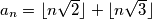 ,
,  , ima beskonačno mnogo parnih i beskonačno mnogo neparnih.
, ima beskonačno mnogo parnih i beskonačno mnogo neparnih.
Dokažite da među brojevima $a_n = \lfloor{n\sqrt{2}}\rfloor + \lfloor{n\sqrt{3}}\rfloor$, $n \in \mathbb{N}$, ima beskonačno mnogo parnih i beskonačno mnogo neparnih.
Izvor: Izborno natjecanje 2007.