Školjka

%V0 Dokažite da sjecište visina šiljastokutnog trokuta $ABC$ s danim kutovima $\alpha $, $\beta $ i $\gamma $, dijeli njegovu visinu iz vrha $A$ u omjeru $ \dfrac{\cos \alpha}{\cos \beta \cos \gamma }$.

%V0 Za koje trokute vrijedi jednakost $$ \tg (\alpha -\beta )+\tg (\beta -\gamma )+\tg (\gamma -\alpha )=0, $$ ako su $\alpha $, $\beta $ i $\gamma $, kutovi trokuta?

%V0 Ako je $\alpha +\beta +\gamma =\pi $, dokažite sljedeći trigonometrijski identitet $$ \sin \alpha +\sin \beta +\sin \gamma =4\cos \frac{\alpha }{2}\cos \frac{\beta }{2}\cos \frac{\gamma }{2}. $$

%V0 Za kutove $\alpha$, $\beta$, $\gamma$ trokuta $ABC$ vrijedi $$ \cos^2\alpha+\cos^2\beta+\cos^2\gamma=1. $$ Dokaži da je trokut pravokutan.

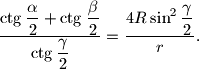
%V0 Pokaži da za svaki trokut s kutovima $\alpha$, $\beta$ i $\gamma$ te polumjerima $r$ i $R$ upisane i opisane kružnice redom, vrijedi jednakost $$ \dfrac{\ctg\dfrac{\alpha}{2}+\ctg\dfrac{\beta}{2}} {\ctg\dfrac{\gamma}{2}}=\dfrac{4R\sin^2\dfrac{\gamma}{2}}{r}. $$

%V0 Dokaži da suma kotangensa kutova trokuta ne može biti jednaka nuli.