Initially, only the integer 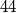 is written on a board. An integer a on the board can be re- placed with four pairwise different integers
is written on a board. An integer a on the board can be re- placed with four pairwise different integers 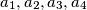 such that the arithmetic mean
such that the arithmetic mean 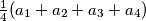 of the four new integers is equal to the number
of the four new integers is equal to the number  . In a step we simultaneously replace all the integers on the board in the above way. After
. In a step we simultaneously replace all the integers on the board in the above way. After 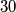 steps we end up with
steps we end up with 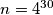 integers
integers 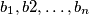 on the board. Prove that
on the board. Prove that 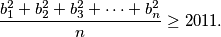
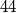 is written on a board. An integer a on the board can be re- placed with four pairwise different integers
is written on a board. An integer a on the board can be re- placed with four pairwise different integers 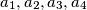 such that the arithmetic mean
such that the arithmetic mean 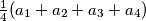 of the four new integers is equal to the number
of the four new integers is equal to the number  . In a step we simultaneously replace all the integers on the board in the above way. After
. In a step we simultaneously replace all the integers on the board in the above way. After 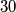 steps we end up with
steps we end up with 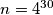 integers
integers 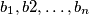 on the board. Prove that
on the board. Prove that 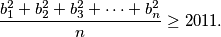
Let  be an integer. John and Mary play the following game: First John labels the sides of a regular
be an integer. John and Mary play the following game: First John labels the sides of a regular  -gon with the numbers
-gon with the numbers 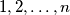 in whatever order he wants, using each number exactly once. Then Mary divides this
in whatever order he wants, using each number exactly once. Then Mary divides this  -gon into triangles by drawing
-gon into triangles by drawing 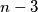 diagonals which do not intersect each other inside the
diagonals which do not intersect each other inside the  -gon. All these diagonals are labeled with number
-gon. All these diagonals are labeled with number  . Into each of the triangles the product of the numbers on its sides is written. Let S be the sum of those
. Into each of the triangles the product of the numbers on its sides is written. Let S be the sum of those 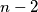 products.
products.
Determine the value of if Mary wants the number
if Mary wants the number  to be as small as possible and John wants
to be as small as possible and John wants  to be as large as possible and if they both make the best possible choices.
to be as large as possible and if they both make the best possible choices.
 be an integer. John and Mary play the following game: First John labels the sides of a regular
be an integer. John and Mary play the following game: First John labels the sides of a regular  -gon with the numbers
-gon with the numbers 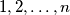 in whatever order he wants, using each number exactly once. Then Mary divides this
in whatever order he wants, using each number exactly once. Then Mary divides this  -gon into triangles by drawing
-gon into triangles by drawing 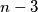 diagonals which do not intersect each other inside the
diagonals which do not intersect each other inside the  -gon. All these diagonals are labeled with number
-gon. All these diagonals are labeled with number  . Into each of the triangles the product of the numbers on its sides is written. Let S be the sum of those
. Into each of the triangles the product of the numbers on its sides is written. Let S be the sum of those 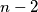 products.
products.Determine the value of
 if Mary wants the number
if Mary wants the number  to be as small as possible and John wants
to be as small as possible and John wants  to be as large as possible and if they both make the best possible choices.
to be as large as possible and if they both make the best possible choices. In a plane the circles 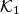 and
and 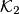 with centers
with centers 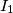 and
and 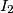 , respectively, intersect in two points
, respectively, intersect in two points  and
and  . Assume that
. Assume that 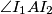 is obtuse. The tangent to
is obtuse. The tangent to 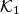 in
in  intersects
intersects 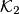 again in
again in  and the tangent to
and the tangent to 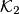 in
in  intersects
intersects 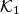 again in
again in  . Let
. Let 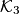 be the circumcircle of the triangle
be the circumcircle of the triangle  . Let
. Let  be the midpoint of that arc
be the midpoint of that arc  of
of 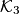 that contains
that contains  . The lines
. The lines  and
and  intersect
intersect 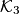 again in
again in  and
and  , respectively. Prove that the line
, respectively. Prove that the line 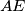 is perpendicular to
is perpendicular to 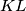 .
.
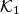 and
and 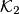 with centers
with centers 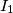 and
and 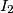 , respectively, intersect in two points
, respectively, intersect in two points  and
and  . Assume that
. Assume that 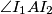 is obtuse. The tangent to
is obtuse. The tangent to 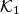 in
in  intersects
intersects 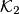 again in
again in  and the tangent to
and the tangent to 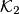 in
in  intersects
intersects 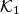 again in
again in  . Let
. Let 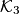 be the circumcircle of the triangle
be the circumcircle of the triangle  . Let
. Let  be the midpoint of that arc
be the midpoint of that arc  of
of 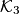 that contains
that contains  . The lines
. The lines  and
and  intersect
intersect 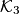 again in
again in  and
and  , respectively. Prove that the line
, respectively. Prove that the line 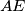 is perpendicular to
is perpendicular to 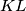 .
. Let  be an integer. At a MEMO-like competition, there are
be an integer. At a MEMO-like competition, there are 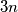 participants, there are n languages spoken, and each participant speaks exactly three different languages. Prove that at least
participants, there are n languages spoken, and each participant speaks exactly three different languages. Prove that at least 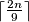 of the spoken languages can be chosen in such a way that no participant speaks more than two of the chosen languages.
of the spoken languages can be chosen in such a way that no participant speaks more than two of the chosen languages.
Note. is the smallest integer which is greater than or equal to
is the smallest integer which is greater than or equal to  .
.
 be an integer. At a MEMO-like competition, there are
be an integer. At a MEMO-like competition, there are 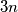 participants, there are n languages spoken, and each participant speaks exactly three different languages. Prove that at least
participants, there are n languages spoken, and each participant speaks exactly three different languages. Prove that at least 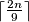 of the spoken languages can be chosen in such a way that no participant speaks more than two of the chosen languages.
of the spoken languages can be chosen in such a way that no participant speaks more than two of the chosen languages.Note.
 is the smallest integer which is greater than or equal to
is the smallest integer which is greater than or equal to  .
. Let  be an acute triangle. Denote by
be an acute triangle. Denote by 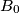 and
and 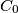 the feet of the altitudes from vertices
the feet of the altitudes from vertices  and
and  , respectively. Let
, respectively. Let  be a point inside the triangle
be a point inside the triangle  such that the line
such that the line 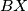 is tangent to the circumcircle of the triangle
is tangent to the circumcircle of the triangle 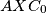 and the line
and the line 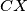 is tangent to the circumcircle of the triangle
is tangent to the circumcircle of the triangle 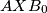 . Show that the line
. Show that the line 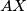 is perpendicular to
is perpendicular to  .
.
 be an acute triangle. Denote by
be an acute triangle. Denote by 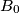 and
and 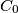 the feet of the altitudes from vertices
the feet of the altitudes from vertices  and
and  , respectively. Let
, respectively. Let  be a point inside the triangle
be a point inside the triangle  such that the line
such that the line 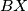 is tangent to the circumcircle of the triangle
is tangent to the circumcircle of the triangle 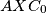 and the line
and the line 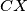 is tangent to the circumcircle of the triangle
is tangent to the circumcircle of the triangle 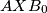 . Show that the line
. Show that the line 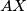 is perpendicular to
is perpendicular to  .
.  Školjka
Školjka  and
and  , with
, with 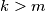 , be positive integers such that the number
, be positive integers such that the number 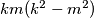 is divisible by
is divisible by  . Prove that
. Prove that 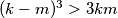 .
. 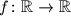 such that the equality
such that the equality 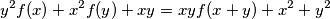 holds for all
holds for all 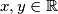 , where
, where 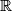 is the set of real numbers.
is the set of real numbers. 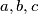 be positive real numbers such that
be positive real numbers such that 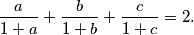
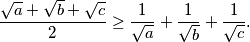
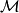 be the set
be the set 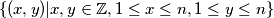 of points in the plane.
of points in the plane. 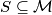 which does not contain three distinct points being the vertices of a right triangle?
which does not contain three distinct points being the vertices of a right triangle? 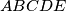 be a convex pentagon with all five sides equal in length. The diagonals
be a convex pentagon with all five sides equal in length. The diagonals 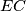 meet in
meet in 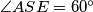 . Prove that
. Prove that 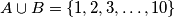 . Show that there exist elements
. Show that there exist elements 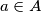 and
and 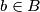 such that the number
such that the number 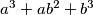 is divisible by
is divisible by 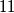 .
. 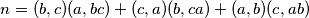 holds. Prove that there exist
holds. Prove that there exist 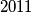 consecutive positive integers which are amazing.
consecutive positive integers which are amazing.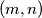 we denote the greatest common divisor of positive integers
we denote the greatest common divisor of positive integers