A set of balls contains  balls which are labeled with numbers
balls which are labeled with numbers 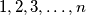 . We are given
. We are given  such sets. We want to colour the balls with two colours, black and white in such a way, that
such sets. We want to colour the balls with two colours, black and white in such a way, that
(a) the balls labeled with the same number are of the same colour,
(b) any subset of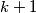 balls with (not necessarily different) labels
balls with (not necessarily different) labels 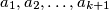 satisfying the condition
satisfying the condition 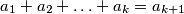 , contains at least one ball of each colour.
, contains at least one ball of each colour.
Find, depending on the greatest possible number
the greatest possible number  which admits such a colouring.
which admits such a colouring.
 balls which are labeled with numbers
balls which are labeled with numbers 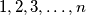 . We are given
. We are given  such sets. We want to colour the balls with two colours, black and white in such a way, that
such sets. We want to colour the balls with two colours, black and white in such a way, that (a) the balls labeled with the same number are of the same colour,
(b) any subset of
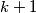 balls with (not necessarily different) labels
balls with (not necessarily different) labels 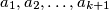 satisfying the condition
satisfying the condition 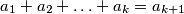 , contains at least one ball of each colour.
, contains at least one ball of each colour. Find, depending on
 the greatest possible number
the greatest possible number  which admits such a colouring.
which admits such a colouring. A tetrahedron is called a MEMO-tetrahedron if all six sidelengths are different positive integers where one of them is  and one of them is
and one of them is  . Let
. Let 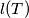 be the sum of the sidelengths of the tetrahedron
be the sum of the sidelengths of the tetrahedron  .
.
(a) Find all positive integers so that there exists a MEMO-Tetrahedron
so that there exists a MEMO-Tetrahedron  with
with 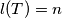 .
.
(b) How many pairwise non-congruent MEMO-tetrahedrons satisfying
satisfying 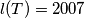 exist? Two tetrahedrons are said to be non-congruent if one cannot be obtained from the other by a composition of reflections in planes, translations and rotations. (It is not neccessary to prove that the tetrahedrons are not degenerate, i.e. that they have a positive volume).
exist? Two tetrahedrons are said to be non-congruent if one cannot be obtained from the other by a composition of reflections in planes, translations and rotations. (It is not neccessary to prove that the tetrahedrons are not degenerate, i.e. that they have a positive volume).
 and one of them is
and one of them is  . Let
. Let 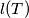 be the sum of the sidelengths of the tetrahedron
be the sum of the sidelengths of the tetrahedron  .
. (a) Find all positive integers
 so that there exists a MEMO-Tetrahedron
so that there exists a MEMO-Tetrahedron  with
with 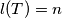 .
. (b) How many pairwise non-congruent MEMO-tetrahedrons
 satisfying
satisfying 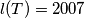 exist? Two tetrahedrons are said to be non-congruent if one cannot be obtained from the other by a composition of reflections in planes, translations and rotations. (It is not neccessary to prove that the tetrahedrons are not degenerate, i.e. that they have a positive volume).
exist? Two tetrahedrons are said to be non-congruent if one cannot be obtained from the other by a composition of reflections in planes, translations and rotations. (It is not neccessary to prove that the tetrahedrons are not degenerate, i.e. that they have a positive volume).  Školjka
Školjka 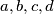 be positive real numbers with
be positive real numbers with 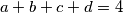 .
. 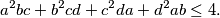
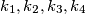 four smaller circles with their centres
four smaller circles with their centres 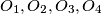 respectively, on
respectively, on 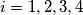 and
and 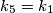 the circles
the circles 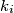 and
and 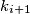 meet at
meet at 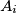 and
and 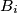 such that
such that 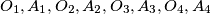 lie in that order on
lie in that order on 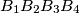 is a rectangle.
is a rectangle. 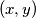 of positive integers satisfying the equation
of positive integers satisfying the equation 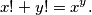
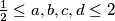 and
and 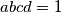 . Find the maximum value of
. Find the maximum value of 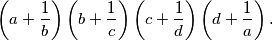
 of five points in the plane, no three of them being collinear, let
of five points in the plane, no three of them being collinear, let 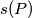 be the numbers of acute triangles formed by vertices in
be the numbers of acute triangles formed by vertices in  so that
so that  is a multiple of
is a multiple of 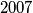 .
.