Let 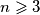 be an integer. An inner diagonal of a simple n-gon is a diagonal that is contained in the
be an integer. An inner diagonal of a simple n-gon is a diagonal that is contained in the  -gon. Denote by
-gon. Denote by 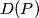 the number of all inner diagonals of a simple
the number of all inner diagonals of a simple  -gon
-gon  and by
and by 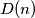 the least possible value of
the least possible value of 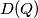 , where
, where  is a simple
is a simple  -gon. Prove that no two inner diagonals of
-gon. Prove that no two inner diagonals of  intersect (except possibly at a common endpoint) if and only if
intersect (except possibly at a common endpoint) if and only if 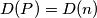 .
.
Remark: A simple  -gon is a non-self-intersecting polygon with
-gon is a non-self-intersecting polygon with  vertices. A polygon is not necessarily convex.
vertices. A polygon is not necessarily convex.
There are  students standing in line in positions
students standing in line in positions  to
to  . While the teacher looks away, some students change their positions. When the teacher looks back, they are standing in line again. If a student who was initially in position
. While the teacher looks away, some students change their positions. When the teacher looks back, they are standing in line again. If a student who was initially in position  is now in position
is now in position  , we say the student moved for
, we say the student moved for 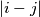 steps. Determine the maximal sum of steps of all students that they can achieve.
steps. Determine the maximal sum of steps of all students that they can achieve.
Let  be the incentre of triangle
be the incentre of triangle  with
with 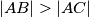 and let the line
and let the line 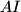 intersect the side
intersect the side  at
at  . Suppose that point
. Suppose that point  lies on the segment
lies on the segment  and satisfies
and satisfies 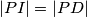 . Further, let
. Further, let 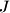 be the point obtained by reflecting
be the point obtained by reflecting  over the perpendicular bisector of
over the perpendicular bisector of  , and let
, and let  be the other intersection of the circumcircles of the triangles
be the other intersection of the circumcircles of the triangles  and
and 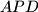 . Prove that
. Prove that 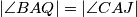 .
.
 Školjka
Školjka 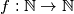 such that for all positive integers
such that for all positive integers  and
and  , exactly one of the following equations is true:
, exactly one of the following equations is true: 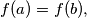
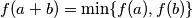 .
.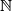 denotes the set of all positive integers. A function
denotes the set of all positive integers. A function 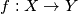 is said to be surjective if for every
is said to be surjective if for every 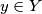 there exists
there exists 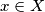 such that
such that 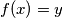 .
.  be a cyclic quadrilateral. Let
be a cyclic quadrilateral. Let  be the intersection of lines parallel to
be the intersection of lines parallel to  and
and  passing through points
passing through points  and
and  , respectively. The lines
, respectively. The lines 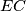 and
and 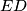 intersect the circumcircle of
intersect the circumcircle of 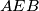 again at
again at  and
and  , respectively. Prove that points
, respectively. Prove that points  ,
, 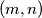 for which there exist relatively prime integers
for which there exist relatively prime integers 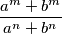 is an integer.
is an integer. 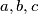 such that
such that 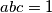 the following inequality holds:
the following inequality holds: 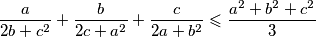
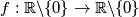 such that
such that 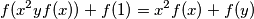 holds for all nonzero real numbers
holds for all nonzero real numbers  and
and  .
.  be a positive integer. In each of the
be a positive integer. In each of the 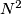 unit squares of an
unit squares of an 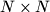 board, one of the two diagonals is drawn. The drawn diagonals divide the
board, one of the two diagonals is drawn. The drawn diagonals divide the  regions. For each
regions. For each  and
and  lie in the interior of
lie in the interior of 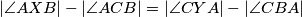 holds, the line
holds, the line  passes through
passes through 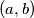 such that
such that 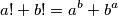
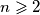 be an integer. Determine the number of positive integers
be an integer. Determine the number of positive integers  such that
such that 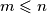 and
and 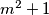 is divisible by
is divisible by