A tract of land in the shape of an 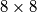 square, whose sides are oriented north–south and east–west, consists of
square, whose sides are oriented north–south and east–west, consists of 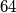 smaller
smaller 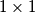 square plots. There can be at most one house on each of the individual plots. A house can only occupy a single
square plots. There can be at most one house on each of the individual plots. A house can only occupy a single 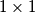 square plot.
square plot.
A house is said to be blocked from sunlight if there are three houses on the plots immediately to its east, west and south.
What is the maximum number of houses that can simultaneously exist, such that none of them is blocked from sunlight?
Remark: By definition, houses on the east, west and south borders are never blocked from sunlight.
A class of high school students wrote a test. Every question was graded as either  point for a correct answer or
point for a correct answer or  points otherwise. It is known that each question was answered correctly by at least one student and the students did not all achieve the same total score.
points otherwise. It is known that each question was answered correctly by at least one student and the students did not all achieve the same total score.
Prove that there was a question on the test with the following property: The students who answered the question correctly got a higher average test score than those who did not.
Let  be an acute-angled triangle with
be an acute-angled triangle with 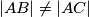 , and let
, and let  be its circumcentre. The line
be its circumcentre. The line 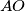 intersects the circumcircle
intersects the circumcircle  of
of  a second time in point
a second time in point  , and the line
, and the line  in point
in point  . The circumcircle of
. The circumcircle of 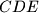 intersects the line
intersects the line  a second time in point
a second time in point  . The line
. The line 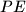 intersects the line
intersects the line  in point
in point  . The line through
. The line through  parallel to
parallel to 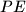 intersects the altitude of the triangle
intersects the altitude of the triangle  that passes through
that passes through  in point
in point  .
.
Prove that 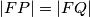 .
.
 Školjka
Školjka 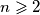 be an integer and
be an integer and 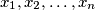 be real numbers satisfying
be real numbers satisfying 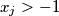 for
for 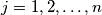 and
and 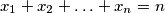
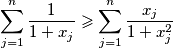 and determine when equality holds.
and determine when equality holds. 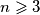 positive integers written on a blackboard. A move consists of choosing three numbers
positive integers written on a blackboard. A move consists of choosing three numbers  ,
,  ,
,  on the blackboard such that they are the sides of a non-degenerate non-equilateral triangle and replacing them by
on the blackboard such that they are the sides of a non-degenerate non-equilateral triangle and replacing them by  ,
,  and
and  .
.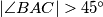 and with circumcentre
and with circumcentre  lie on a circle and
lie on a circle and 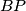 is perpendicular to
is perpendicular to 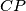 . The point
. The point 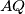 is parallel to
is parallel to 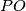 .
.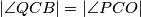 .
. 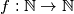 such that
such that 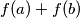 divides
divides 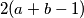 for all
for all 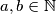 .
.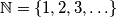 denotes the set of positive integers.
denotes the set of positive integers. 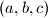 of real numbers satisfying the system of equations
of real numbers satisfying the system of equations 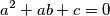
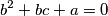
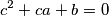
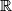 denote the set of real numbers. Determine all functions
denote the set of real numbers. Determine all functions 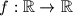 such that
such that 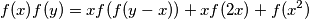 holds for all real numbers
holds for all real numbers  and
and  .
.  ,
,  ,
,  are the midpoints of the sides
are the midpoints of the sides  touches the side
touches the side  , which passes through the midpoint of segment
, which passes through the midpoint of segment  and is perpendicular to
and is perpendicular to 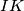 , intersects the line
, intersects the line 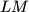 at point
at point 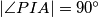 .
.  is called a Mozartian number if the numbers
is called a Mozartian number if the numbers 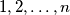 together contain an even number of each digit (in base
together contain an even number of each digit (in base  ).
). 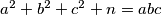 , where
, where 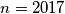 .
. 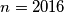 ,
,  for every solution
for every solution