Dokaži da je broj jedinica u svim neuređenim particijama nekog prirodnog broja jednak:
a) sumi brojeva različitih elemenata po svim particijama
b) sumi razlika, po svim particijama, najvećeg i drugog po veličini elementa
Neuređena particija prirodnog broja  je multiskup prirodnih brojeva takav da je zbroj njegovih elemenata
je multiskup prirodnih brojeva takav da je zbroj njegovih elemenata  .
.
(Ivan Novak, Borna Šimić)
Dokaži da je broj jedinica u svim neuređenim particijama nekog prirodnog broja jednak:
a) sumi brojeva različitih elemenata po svim particijama
b) sumi razlika, po svim particijama, najvećeg i drugog po veličini elementa
Neuređena particija prirodnog broja $n$ je multiskup prirodnih brojeva takav da je zbroj njegovih elemenata $n$.
\begin{flushright}\emph{(Ivan Novak, Borna Šimić)}\end{flushright}
 je multiskup prirodnih brojeva takav da je zbroj njegovih elemenata
je multiskup prirodnih brojeva takav da je zbroj njegovih elemenata  .
. Školjka
Školjka 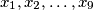 nenegativni realni brojevi takvi da
nenegativni realni brojevi takvi da 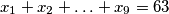 . Dokaži:
. Dokaži: ![12 \leqslant \sqrt[3]{1+x_1} + \sqrt[3]{1+x_2} + \ldots + \sqrt[3]{1+x_9} \leqslant 18](/media/m/b/3/c/b3c01db2fe544261680d6c646977f08d.png)
 takav da mu je
takav da mu je  najduža stranica. Neka je
najduža stranica. Neka je  njegova opisana kružnica, a
njegova opisana kružnica, a 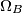 i
i 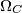 kružnice središta
kružnice središta  ,
,  radijusa
radijusa 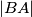 ,
, 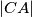 redom. Dokaži da tri sjecišta kružnica
redom. Dokaži da tri sjecišta kružnica 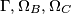 koja nisu
koja nisu  čine trokut sličan trokutu
čine trokut sličan trokutu  vrijedi da nema cjelobrojne nultočke te da za svaki prosti
vrijedi da nema cjelobrojne nultočke te da za svaki prosti  postoji
postoji  takav da
takav da 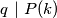 .
. ?
?