Školjka

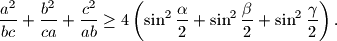
%V0 Ako su $\alpha $, $\beta $ i $\gamma $ kutovi trokuta s duljinama stranicama $a$, $b$ i $c$, dokažite nejednakost $$ \frac{a^2}{bc}+\frac{b^2}{ca}+\frac{c^2}{ab}\geq 4\left(\sin^2\frac{\alpha }{2}+\sin ^2\frac{\beta }{2} +\sin ^2\frac{\gamma}{2}\right). $$