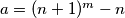
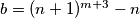
Neka su i prirodni brojevi, i . Dokažite da su i relativno prosti ako nije djeljiv s . Odredite sve brojeve i za koje i nisu relativno prosti.
%V0
Neka su $m$ i $n$ prirodni brojevi, $a = (n+1)^m - n$ i $b = (n+1)^{m+3} - n$.
$(a)$ Dokažite da su $a$ i $b$ relativno prosti ako $m$ nije djeljiv s $3$.
$(b)$ Odredite sve brojeve $m$ i $n$ za koje $a$ i $b$ nisu relativno prosti.
Školjka 
i 
prirodni brojevi, 
i 
.
Dokažite da su 
i 
relativno prosti ako 
.
Odredite sve brojeve