Državno natjecanje 1996 SŠ1 2
Dodao/la:
arhiva1. travnja 2012. Brojevi

,

,

,

zadovoljavaju relaciju
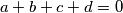
. Neka je
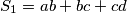
i
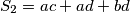
. Pokažite da je
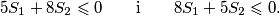
%V0
Brojevi $a$, $b$, $c$, $d$ zadovoljavaju relaciju $a+b+c+d=0$. Neka je $S_1=ab+bc+cd$ i $S_2=ac+ad+bd$. Pokažite da je $$5S_1+8S_2 \leqslant 0 \qquad \text{i} \qquad 8S_1+5S_2 \leqslant 0 \text{.}$$
Izvor: Državno natjecanje iz matematike 1996