Državno natjecanje 1999 SŠ2 4
Dodao/la:
arhiva1. travnja 2012. na jednom turniru sudjelovalo je

kosarkaskih ekipa. svaka ekipa odigrala je sa svakom drugom tocno jednu utakmicu. nerijesenih ishoda nije bilo. ako na kraju turnira

-ita ekipa ima
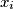
pobjeda i
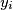
poraza
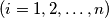
dokazite da je
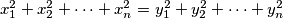
%V0
na jednom turniru sudjelovalo je $n$ kosarkaskih ekipa. svaka ekipa odigrala je sa svakom drugom tocno jednu utakmicu. nerijesenih ishoda nije bilo. ako na kraju turnira $i$-ita ekipa ima $x_i$ pobjeda i $y_i$ poraza $(i = 1, 2, \dots, n)$ dokazite da je
$x_1^2 + x_2^2 + \dots + x_n^2 = y_1^2 + y_2^2 + \dots + y_n^2$
Izvor: Državno natjecanje iz matematike 1999