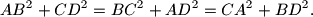Slični zadaci
An isosceles trapezoid with bases  and
and  and altitude
and altitude  is given.
is given.
a) On the axis of symmetry of this trapezoid, find all points such that both legs of the trapezoid subtend right angles at
such that both legs of the trapezoid subtend right angles at  ;
;
b) Calculate the distance of from either base;
from either base;
c) Determine under what conditions such points actually exist. Discuss various cases that might arise.
actually exist. Discuss various cases that might arise.
 and
and  and altitude
and altitude  is given.
is given. a) On the axis of symmetry of this trapezoid, find all points
 such that both legs of the trapezoid subtend right angles at
such that both legs of the trapezoid subtend right angles at  ;
; b) Calculate the distance of
 from either base;
from either base; c) Determine under what conditions such points
 actually exist. Discuss various cases that might arise.
actually exist. Discuss various cases that might arise. Given the tetrahedron  whose edges
whose edges  and
and  have lengths
have lengths  and
and  respectively. The distance between the skew lines
respectively. The distance between the skew lines  and
and  is
is  , and the angle between them is
, and the angle between them is  . Tetrahedron
. Tetrahedron  is divided into two solids by plane
is divided into two solids by plane  , parallel to lines
, parallel to lines  and
and  . The ratio of the distances of
. The ratio of the distances of  from
from  and
and  is equal to
is equal to  . Compute the ratio of the volumes of the two solids obtained.
. Compute the ratio of the volumes of the two solids obtained.
 whose edges
whose edges  and
and  have lengths
have lengths  and
and  respectively. The distance between the skew lines
respectively. The distance between the skew lines  and
and  is
is  , and the angle between them is
, and the angle between them is  . Tetrahedron
. Tetrahedron  is divided into two solids by plane
is divided into two solids by plane  , parallel to lines
, parallel to lines  and
and  . The ratio of the distances of
. The ratio of the distances of  from
from  and
and  is equal to
is equal to  . Compute the ratio of the volumes of the two solids obtained.
. Compute the ratio of the volumes of the two solids obtained.  Školjka
Školjka 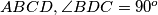 and the foot of the perpendicular from
and the foot of the perpendicular from  to
to  is the intersection of the altitudes of
is the intersection of the altitudes of 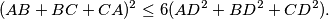 When do we have equality?
When do we have equality?  in the interior of the segment
in the interior of the segment  in
in 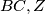 in
in  in
in  .
. 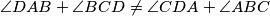 , then prove none of the closed paths
, then prove none of the closed paths  has minimal length;
has minimal length; 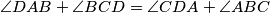 , then there are infinitely many shortest paths
, then there are infinitely many shortest paths 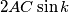 , where
, where 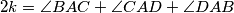 .
.