IMO Shortlist 1971 problem 7
Dodao/la:
arhiva2. travnja 2012. All faces of the tetrahedron

are acute-angled. Take a point

in the interior of the segment

, and similarly
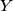
in
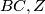
in

and

in
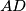
.
a.) If
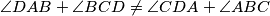
, then prove none of the closed paths
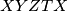
has minimal length;
b.) If
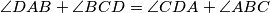
, then there are infinitely many shortest paths
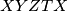
, each with length
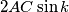
, where
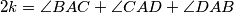
.
%V0
All faces of the tetrahedron $ABCD$ are acute-angled. Take a point $X$ in the interior of the segment $AB$, and similarly $Y$ in $BC, Z$ in $CD$ and $T$ in $AD$.
a.) If $\angle DAB+\angle BCD\ne\angle CDA+\angle ABC$, then prove none of the closed paths $XYZTX$ has minimal length;
b.) If $\angle DAB+\angle BCD=\angle CDA+\angle ABC$, then there are infinitely many shortest paths $XYZTX$, each with length $2AC\sin k$, where $2k=\angle BAC+\angle CAD+\angle DAB$.
Izvor: Međunarodna matematička olimpijada, shortlist 1971