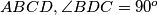
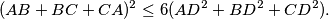
In the tetrahedron and the foot of the perpendicular from to is the intersection of the altitudes of . Prove that: When do we have equality?
%V0
In the tetrahedron $ABCD,\angle BDC=90^o$ and the foot of the perpendicular from $D$ to $ABC$ is the intersection of the altitudes of $ABC$. Prove that: $$(AB+BC+CA)^2\le6(AD^2+BD^2+CD^2).$$ When do we have equality?
Izvor: Međunarodna matematička olimpijada, shortlist 1970
Školjka 
and the foot of the perpendicular from 
to 
is the intersection of the altitudes of 
When do we have equality?