Slični zadaci
Let  be a regular
be a regular 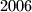 -gon. A diagonal is called good if its endpoints divide the boundary of
-gon. A diagonal is called good if its endpoints divide the boundary of  into two parts, each composed of an odd number of sides of
into two parts, each composed of an odd number of sides of  . The sides of
. The sides of  are also called good.
are also called good.
Suppose has been dissected into triangles by
has been dissected into triangles by 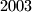 diagonals, no two of which have a common point in the interior of
diagonals, no two of which have a common point in the interior of  . Find the maximum number of isosceles triangles having two good sides that could appear in such a configuration.
. Find the maximum number of isosceles triangles having two good sides that could appear in such a configuration.
 be a regular
be a regular 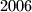 -gon. A diagonal is called good if its endpoints divide the boundary of
-gon. A diagonal is called good if its endpoints divide the boundary of  into two parts, each composed of an odd number of sides of
into two parts, each composed of an odd number of sides of  . The sides of
. The sides of  are also called good.
are also called good. Suppose
 has been dissected into triangles by
has been dissected into triangles by 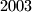 diagonals, no two of which have a common point in the interior of
diagonals, no two of which have a common point in the interior of  . Find the maximum number of isosceles triangles having two good sides that could appear in such a configuration.
. Find the maximum number of isosceles triangles having two good sides that could appear in such a configuration. Let  be a triangle with circumcentre
be a triangle with circumcentre  . The points
. The points  and
and  are interior points of the sides
are interior points of the sides  and
and  respectively. Let
respectively. Let 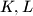 and
and  be the midpoints of the segments
be the midpoints of the segments 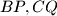 and
and  . respectively, and let
. respectively, and let  be the circle passing through
be the circle passing through 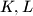 and
and  . Suppose that the line
. Suppose that the line  is tangent to the circle
is tangent to the circle  . Prove that
. Prove that 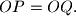
Proposed by Sergei Berlov, Russia
 be a triangle with circumcentre
be a triangle with circumcentre  . The points
. The points  and
and  are interior points of the sides
are interior points of the sides  and
and  respectively. Let
respectively. Let 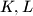 and
and  be the midpoints of the segments
be the midpoints of the segments 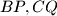 and
and  . respectively, and let
. respectively, and let  be the circle passing through
be the circle passing through 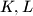 and
and  . Suppose that the line
. Suppose that the line  is tangent to the circle
is tangent to the circle  . Prove that
. Prove that 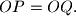
Proposed by Sergei Berlov, Russia
 Školjka
Školjka 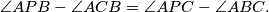
 ,
,  be the incenters of triangles
be the incenters of triangles 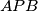 ,
, 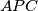 , respectively. Show that the lines
, respectively. Show that the lines 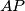 ,
,  ,
, 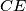 meet at a point.
meet at a point.  has centre
has centre  is a diameter of
is a diameter of  be a point of
be a point of 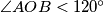 . Let
. Let  . The line through
. The line through 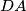 meets the line
meets the line  at
at  . The perpendicular bisector of
. The perpendicular bisector of 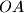 meets
meets  . Prove that
. Prove that 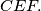
 be an integer. Let
be an integer. Let 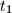 ,
, 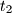 , ...,
, ..., 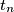 be positive real numbers such that
be positive real numbers such that 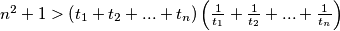 .
. 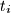 ,
, 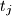 ,
, 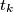 are side lengths of a triangle for all
are side lengths of a triangle for all  ,
,  ,
,  with
with 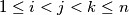 .
. 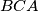 intersects the circumcircle again at
intersects the circumcircle again at  , the perpendicular bisector of
, the perpendicular bisector of  and the midpoint of
and the midpoint of  . Prove that the triangles
. Prove that the triangles 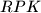 and
and 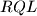 have the same area.
have the same area. 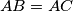 . The angle bisectors of
. The angle bisectors of 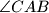 and
and 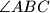 meet the sides
meet the sides 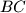 and
and 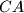 at
at 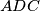 . Suppose that
. Suppose that 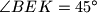 . Find all possible values of
. Find all possible values of