Slični zadaci
Kružnice  i
i  sijeku se u točkama
sijeku se u točkama  i
i  . Tangenta kružnice
. Tangenta kružnice  povučena iz točke
povučena iz točke  siječe kružnicu
siječe kružnicu  u točki
u točki  , a tangenta kružnice
, a tangenta kružnice  povućena iz točke
povućena iz točke  siječe kružnicu
siječe kružnicu  u točki
u točki  . Polupravac kroz točku
. Polupravac kroz točku  , koji leži unutar kuta
, koji leži unutar kuta 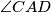 , siječe kružnicu
, siječe kružnicu  u točki
u točki  , kružnicu
, kružnicu  u točki
u točki  i kružnicu opisanu trokutu
i kružnicu opisanu trokutu  u točki
u točki  . Dokaži da je udaljenost točaka
. Dokaži da je udaljenost točaka  i
i  jednaka udaljenosti točaka
jednaka udaljenosti točaka  i
i  .
.
 i
i  sijeku se u točkama
sijeku se u točkama  i
i  . Tangenta kružnice
. Tangenta kružnice  povučena iz točke
povučena iz točke  siječe kružnicu
siječe kružnicu  u točki
u točki  , a tangenta kružnice
, a tangenta kružnice  povućena iz točke
povućena iz točke  siječe kružnicu
siječe kružnicu  u točki
u točki  . Polupravac kroz točku
. Polupravac kroz točku  , koji leži unutar kuta
, koji leži unutar kuta 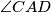 , siječe kružnicu
, siječe kružnicu  u točki
u točki  , kružnicu
, kružnicu  u točki
u točki  i kružnicu opisanu trokutu
i kružnicu opisanu trokutu  u točki
u točki  . Dokaži da je udaljenost točaka
. Dokaži da je udaljenost točaka  i
i  jednaka udaljenosti točaka
jednaka udaljenosti točaka  i
i  .
.  Školjka
Školjka  fiksan. Polovišta stranica
fiksan. Polovišta stranica  i
i  su točke
su točke  redom. Točke
redom. Točke  i
i  su takve da je
su takve da je 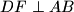 i
i 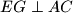 , a
, a 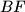 i
i 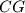 su okomite na
su okomite na  . Dokažite da umnožak
. Dokažite da umnožak  ne ovisi o položaju točke
ne ovisi o položaju točke  ,
,  i
i  stranica trokuta vrijedi
stranica trokuta vrijedi 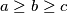 . vrhovi trokuta sredista su triju krugova s nenegativnim polumjerima. nikoja dva kruga nemaju zajednickih unutarnjih tocaka, niti obuhvacaju nikoji od preostala dva vrha trokuta. kolika je maksimalna povrsina koju prekrivaju ta tri kruga?
. vrhovi trokuta sredista su triju krugova s nenegativnim polumjerima. nikoja dva kruga nemaju zajednickih unutarnjih tocaka, niti obuhvacaju nikoji od preostala dva vrha trokuta. kolika je maksimalna povrsina koju prekrivaju ta tri kruga?  i
i  kojem je točka
kojem je točka 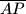 i
i 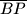 . Točka
. Točka  je presjek dužina
je presjek dužina 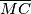 i
i 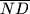 . Dokažite da točke
. Dokažite da točke 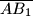 i
i 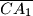 bočnih strana
bočnih strana 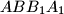 i
i 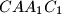 trostrane prizme
trostrane prizme 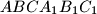 dane su točke
dane su točke 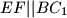 . Nađite omjer duljina dužina
. Nađite omjer duljina dužina 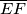 i
i 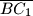 .
.  koji ne sadrži točku
koji ne sadrži točku