Hrvatska matematička olimpijada 1994 - Prvi dan - Zadatak 1
Dodao/la:
mljulj12. travnja 2012. Neka je
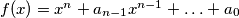
polinom s realnim koeficijentima takav da je
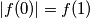
, pri čemu je za svaki njegov korijen

,
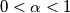
. Dokažite da produkt svih korijena nije veći od
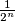
.
%V0
Neka je $f(x)=x^n + a_{n-1}x^{n-1}+ \ldots + a_0$ polinom s realnim koeficijentima takav da je $|f(0)|= f(1)$, pri čemu je za svaki njegov korijen $\alpha$, $0<\alpha<1$. Dokažite da produkt svih korijena nije veći od $\frac{1}{2^n}$.
Izvor: Hrvatska matematička olimpijada 1994.