Hrvatska matematička olimpijada 1994 - Drugi dan - Zadatak 1
Dodao/la:
mljulj12. travnja 2012. Dan je prirodan broj

. Neka je
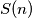
skup kompleksnih brojeva na jediničnoj kružnici u kompleksnoj ravnini sa središtem u točki
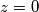
koji zadovoljavaju sljedeću jednakost
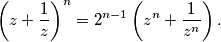
a) Odredite skup
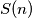
za
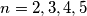
.
b) Odredite gornju granicu (ovisnu o

) za broj elemenata skupa
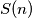
.
%V0
Dan je prirodan broj $n$. Neka je $S(n)$ skup kompleksnih brojeva na jediničnoj kružnici u kompleksnoj ravnini sa središtem u točki $z=0$ koji zadovoljavaju sljedeću jednakost
$$ \left( z+\frac{1}{z} \right)^n=2^{n-1} \left( z^n+\frac{1}{z^n} \right).$$
a) Odredite skup $S(n)$ za $n=2,3,4,5$.
b) Odredite gornju granicu (ovisnu o $n$) za broj elemenata skupa $S(n)$.
Izvor: Hrvatska matematička olimpijada 1994.