Mala olimpijada 1998 zadatak 4
Dodao/la:
mljulj12. travnja 2012. Niz
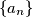
je zadan na ovaj način:
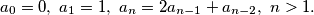
Dokažite da
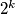
dijeli

ako i samo ako
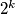
dijeli

.
%V0
Niz $\{ a_n \} $ je zadan na ovaj način:
$$ a_0=0, \ a_1=1, \ a_n=2a_{n-1}+a_{n-2}, \ n>1.$$
Dokažite da $2^k$ dijeli $a_n$ ako i samo ako $2^k$ dijeli $n$.
Izvor: Mala olimpijada 1998 zadatak 2