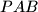
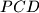
Dvije kružnice sijeku se u točkama i . Ako dva pravca koja prolaze kroz točku sijeku prvu kružnicu u točkama i , a drugu kružnicu u točkama i , dokaži da su trokuti i slični.
%V0
Dvije kružnice sijeku se u točkama $P$ i $Q$. Ako dva pravca koja prolaze kroz točku $Q$ sijeku prvu kružnicu u točkama $A$ i $B$, a drugu kružnicu u točkama $C$ i $D$, dokaži da su trokuti $PAB$ i $PCD$ slični.
Školjka 
i 
. Ako dva pravca koja prolaze kroz točku 
i 
, a drugu kružnicu u točkama 
i 
, dokaži da su trokuti 
i 
slični.