Općinsko natjecanje 2012 SŠ3 6
Dodao/la:
arhiva14. svibnja 2012. Odredi sve vrijednosti realnog parametra

za koje jednadžba
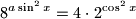
ima točno jedno rješenje u intervalu
![\displaystyle \left[-\frac{\pi}{6},\frac{2\pi}{3}\right]](/media/m/5/3/f/53fe910e355e9d714d0087f501e48819.png)
.
%V0
Odredi sve vrijednosti realnog parametra $a$ za koje jednadžba $$8^{a\sin^2x}=4\cdot 2^{\cos^2{x}}$$ ima točno jedno rješenje u intervalu $\displaystyle \left[-\frac{\pi}{6},\frac{2\pi}{3}\right]$.
Izvor: Općinsko natjecanje iz matematike 2012