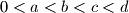
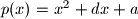
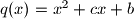
Neka je i neka svaka od kvadratnih funkcija i ima dvije različite realne nultočke.
Dokaži da su sve četiri nultočke međusobno različite.
%V0
Neka je $0 < a < b < c < d$ i neka svaka od kvadratnih funkcija $p(x)=x^2 + dx + a$ i $q(x)=x^2 + cx + b$ ima dvije različite realne nultočke.
Dokaži da su sve četiri nultočke međusobno različite.
Školjka 
i neka svaka od kvadratnih funkcija 
i 
ima dvije različite realne nultočke.