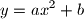
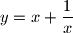
Neka su i realni brojevi. Poznato je da parabola siječe krivulju u točno tri točke. Dokaži da vrijedi .
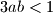
%V0
Neka su $a$ i $b$ realni brojevi. Poznato je da parabola $\displaystyle y=ax^2+b$ siječe krivulju $\displaystyle y=x+\frac 1x$ u točno tri točke. Dokaži da vrijedi $3ab <1$.
Školjka 
i 
realni brojevi. Poznato je da parabola 
siječe krivulju 
u točno tri točke. Dokaži da vrijedi 
.