Dokažite da u svakom trokutu vrijedi nejednakost
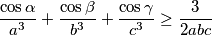
pri čemu su

duljine stranica trokuta, te
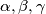
odgovarajući kutovi.
%V0
Dokažite da u svakom trokutu vrijedi nejednakost
$$\frac{\cos\alpha}{a^3} + \frac{\cos\beta}{b^3} + \frac{\cos\gamma}{c^3} \geq \frac{3}{2abc}$$
pri čemu su $a, b, c$ duljine stranica trokuta, te $\alpha, \beta, \gamma$ odgovarajući kutovi.