Državno natjecanje 1996 SŠ4 3
Dodao/la:
arhiva1. travnja 2012. Odredite funkcije
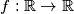
, neprekidne u nuli, koje zadovoljavaju ovu relaciju
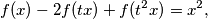
za svako
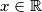
, gdje je
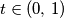
dani fiksan broj.
%V0
Odredite funkcije $f : \mathbb{R} \rightarrow \mathbb{R}$, neprekidne u nuli, koje zadovoljavaju ovu relaciju $$f(x) - 2f(tx) + f(t^2x) = x^2\text{,}$$ za svako $x \in \mathbb{R}$, gdje je $t \in (0,\,1)$ dani fiksan broj.
Izvor: Državno natjecanje iz matematike 1996