Državno natjecanje 1997 SŠ4 3
Dodao/la:
arhiva1. travnja 2012. Dana je funkcija

definirana na pozitivnim cijelim brojevima, koja ima ova svojstva
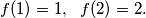
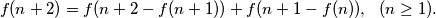

Pokažite da je
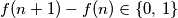
za svaki
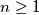
.

Ako je

neparan, pokažite da je
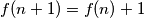
.
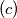
Za dani broj

odredite sve vrijednosti

za koje je
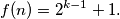
%V0
Dana je funkcija $f$ definirana na pozitivnim cijelim brojevima, koja ima ova svojstva $$f(1)=1,\,\,\,\, f(2)=2\text{.}$$
$$f(n+2)=f(n+2-f(n+1))+f(n+1-f(n)), \,\,\,\, (n \geq 1)\text{.}$$
$(a)$ Pokažite da je $f(n+1)-f(n) \in \{0,\,1\}$ za svaki $n \geq 1$.
$(b)$ Ako je $f(n)$ neparan, pokažite da je $f(n+1)=f(n)+1$.
$(c)$ Za dani broj $k$ odredite sve vrijednosti $n$ za koje je $$f(n)=2^{k-1}+1\text{.}$$
Izvor: Državno natjecanje iz matematike 1997