Neka je

trokut u kojem je najdulja stranica

, a kut
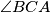
tri puta veći od kuta

. Simetrala vanjskog kuta kod vrha

siječe pravac

u točki

, a simetrala vanjskog kuta kod vrha

siječe pravac

u točki
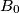
. Ako je
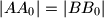
, odredi kutove danog trokuta.
%V0
Neka je $ABC$ trokut u kojem je najdulja stranica $\overline{BC}$, a kut $\angle BCA$ tri puta veći od kuta $\angle ABC$. Simetrala vanjskog kuta kod vrha $A$ siječe pravac $BC$ u točki $A_0$, a simetrala vanjskog kuta kod vrha $B$ siječe pravac $AC$ u točki $B_0$. Ako je $|AA_0| = |BB_0|$, odredi kutove danog trokuta.