Državno natjecanje 1998 SŠ4 2
Dodao/la:
arhiva1. travnja 2012. Neka su

i

prirodni brojevi,

neparan prost broj, takav da
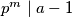
i
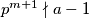
. Dokažite da

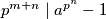
za svaki

,

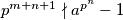
za svaki

.
%V0
Neka su $a$ i $m$ prirodni brojevi, $p$ neparan prost broj, takav da $p^m \mid a - 1$ i $p^{m+1} \nmid a - 1$. Dokažite da
$a)$ $p^{m+n} \mid a^{p^n} - 1$ za svaki $n \in \mathbb{N}$,
$b)$ $p^{m+n+1} \nmid a^{p^n} - 1$ za svaki $n \in \mathbb{N}$.
Izvor: Državno natjecanje iz matematike 1998