Neka je

prirodni broj. Tri kvadrata stranice duljine

spojena su kao na slici. Zatim je svaki od njih podijeljen na
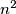
jediničnih kvadratića.
Koliko je ukupno pravokutnika na crtežu nakon podjele na jedinične kvadratiće?
%V0
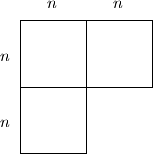
Neka je $n$ prirodni broj. Tri kvadrata stranice duljine $n$ spojena su kao na slici. Zatim je svaki od njih podijeljen na $n^2$ jediničnih kvadratića.
$$$
\setlength{\unitlength}{40pt}
\begin{center}
\begin{picture}(2.3, 2.3)(-0.3, 0)
\put(0, 0){\line(0, 1){2}}
\put(1, 0){\line(0, 1){2}}
\put(2, 1){\line(0, 1){1}}
\put(0, 0){\line(1, 0){1}}
\put(0, 1){\line(1, 0){2}}
\put(0, 2){\line(1, 0){2}}
\put(-0.3, 0.4){$n$}
\put(-0.3, 1.4){$n$}
\put(0.4, 2.2){$n$}
\put(1.4, 2.2){$n$}
\end{picture}
\end{center}
$$$
Koliko je ukupno pravokutnika na crtežu nakon podjele na jedinične kvadratiće?