Državno natjecanje 1999 SŠ4 3
Dodao/la:
arhiva1. travnja 2012. izracunajte sumu
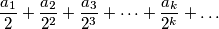
gdje je
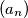
niz brojeva definiran na ovaj nacin:
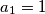
,
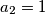
,
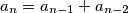
, za
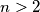
%V0
izracunajte sumu
$\dfrac{a_1}{2} + \dfrac{a_2}{2^2} + \dfrac{a_3}{2^3} + \dots + \dfrac{a_k}{2^k} + \dots$
gdje je $(a_n)$ niz brojeva definiran na ovaj nacin:
$a_1 = 1$, $a_2 = 1$, $a_n = a_{n-1} + a_{n-2}$, za $n > 2$
Izvor: Državno natjecanje iz matematike 1999