Krakovi jednakokračnog trokuta diraju kružnicu čije se središte nalazi na osnovici tog trokuta. Točke i nalaze se na stranicama i redom. Dokažite da je
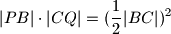
ako i samo ako je tangenta promatrane kružnice.
%V0
Krakovi jednakokračnog trokuta $ABC$ diraju kružnicu čije se središte nalazi na osnovici $\overline{BC}$ tog trokuta. Točke $P$ i $Q$ nalaze se na stranicama $\overline{AB}$ i $\overline{AC}$ redom. Dokažite da je
$$|PB| \cdot |CQ| = (\frac{1}{2} |BC|)^2$$
ako i samo ako je $PQ$ tangenta promatrane kružnice.
Školjka 
diraju kružnicu čije se središte nalazi na osnovici 
tog trokuta. Točke 
i 
nalaze se na stranicama 
i 
redom. Dokažite da je
tangenta promatrane kružnice.