Državno natjecanje 2000 SŠ4 3
Dodao/la:
arhiva1. travnja 2012. Na kružnici je zapisano
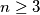
prirodnih brojeva tako da svaki od njih dijeli zbroj dva njemu susjedna broja. Označimo
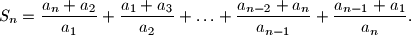
Odredite najveću i najmanju vrijednost od
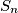
.
%V0
Na kružnici je zapisano $n \geq 3$ prirodnih brojeva tako da svaki od njih dijeli zbroj dva njemu susjedna broja. Označimo
$$S_n = \frac{a_n + a_2}{a_1} + \frac{a_1 + a_3}{a_2} + \ldots + \frac{a_{n-2} + a_n}{a_{n-1}} + \frac{a_{n-1} + a_1}{a_n}.$$
Odredite najveću i najmanju vrijednost od $S_n$.
Izvor: Državno natjecanje iz matematike 2000