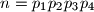
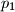
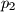
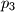
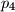
Dan je broj , gdje su , , i četiri različita prosta broja. Njegovi pozitivni cjelobrojni djelitelji su
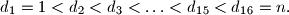
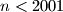
Postoji li , takav da je ?
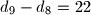
%V0
Dan je broj $n = p_1 p_2 p_3 p_4$, gdje su $p_1$, $p_2$, $p_3$ i $p_4$ četiri različita prosta broja. Njegovi pozitivni cjelobrojni djelitelji su
$$d_1 = 1 < d_2 < d_3 < \ldots < d_{15} < d_{16} = n.$$
Postoji li $n < 2001$, takav da je $d_9 - d_8 = 22$?
Školjka 
, gdje su 
, 
, 
i 
četiri različita prosta broja. Njegovi pozitivni cjelobrojni djelitelji su
, takav da je 
?