Vrhovi kocke u prostornom koordinatnom sustavu s ishodištem

su u točkama
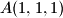
,
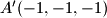
,
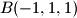
,
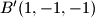
,
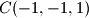
,
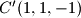
,
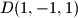
,
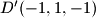
. Točka

je središte kocki opisane sfere. Neka točka

nije na toj sferi i
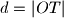
. Označimo s
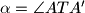
,
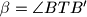
,
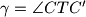
,
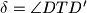
. Dokažite da je
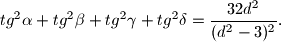
%V0
Vrhovi kocke u prostornom koordinatnom sustavu s ishodištem $O$ su u točkama $A(1,1,1)$, $A^\prime(-1,-1,-1)$, $B(-1,1,1)$, $B^\prime(1,-1,-1)$, $C(-1,-1,1)$, $C^\prime(1,1,-1)$, $D(1,-1,1)$, $D^\prime(-1,1,-1)$. Točka $O$ je središte kocki opisane sfere. Neka točka $T$ nije na toj sferi i $d=|OT|$. Označimo s $\alpha = \angle ATA^\prime$, $\beta = \angle BTB^\prime$, $\gamma = \angle CTC^\prime$, $\delta = \angle DTD^\prime$. Dokažite da je
$$tg^2 \alpha + tg^2 \beta + tg^2 \gamma + tg^2 \delta = \frac{32d^2}{(d^2-3)^2}.$$