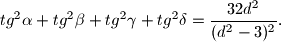Slični zadaci
Na slici su unutar kružnice sa središtem  i polumjerom
i polumjerom  nacrtani lukovi još šest kružnica istog polumjera. U području između dvije susjedne "latice" upisan je niz kružnica s polumjerima
nacrtani lukovi još šest kružnica istog polumjera. U području između dvije susjedne "latice" upisan je niz kružnica s polumjerima 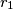 ,
, 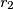 ,
, 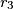 , ..., koje se s početnom kružnicom i susjednim kružnicama u nizu dodiruju redom u točkama
, ..., koje se s početnom kružnicom i susjednim kružnicama u nizu dodiruju redom u točkama 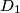 ,
, 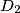 ,
, 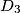 , ... . Za svaki
, ... . Za svaki  izračunajte polumjer
izračunajte polumjer 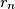 i duljinu
i duljinu 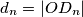 .
.
{{ Greška pri preuzimanju img datoteke. (Nevaljan broj?) }}
 i polumjerom
i polumjerom  nacrtani lukovi još šest kružnica istog polumjera. U području između dvije susjedne "latice" upisan je niz kružnica s polumjerima
nacrtani lukovi još šest kružnica istog polumjera. U području između dvije susjedne "latice" upisan je niz kružnica s polumjerima 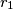 ,
, 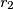 ,
, 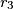 , ..., koje se s početnom kružnicom i susjednim kružnicama u nizu dodiruju redom u točkama
, ..., koje se s početnom kružnicom i susjednim kružnicama u nizu dodiruju redom u točkama 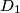 ,
, 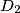 ,
, 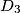 , ... . Za svaki
, ... . Za svaki  izračunajte polumjer
izračunajte polumjer 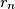 i duljinu
i duljinu 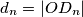 .
.{{ Greška pri preuzimanju img datoteke. (Nevaljan broj?) }}
 Školjka
Školjka  tocka na simetrali kuta
tocka na simetrali kuta  trokuta
trokuta  , a
, a  i
i  redom tocke na stranicama
redom tocke na stranicama  i
i  , takve da je
, takve da je 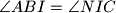 i
i 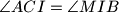 . dokazite da je
. dokazite da je  i točka
i točka  . Za bilo koje dvije različite točke
. Za bilo koje dvije različite točke  i
i  na
na 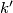 prolazi kroz točke
prolazi kroz točke  . Opišite geometrijsko mjesto točama
. Opišite geometrijsko mjesto točama 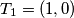 ,
, 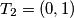 ,
, 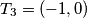 ,
, 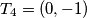 . za svaki
. za svaki  neka je
neka je 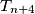 poloviste duzine
poloviste duzine 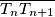 . uz pretpostavku da niz tocaka
. uz pretpostavku da niz tocaka 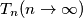 ima granicnu tocku, nadite koordinate te tocke.
ima granicnu tocku, nadite koordinate te tocke. 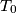 na paraboli
na paraboli 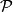 s jednadžbom
s jednadžbom 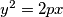 i točka
i točka 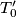 takva da je polovište dužine
takva da je polovište dužine 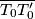 na osi parabole
na osi parabole  na
na 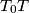 siječe paralelu s osi parabole kroz točku
siječe paralelu s osi parabole kroz točku 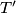 . Što opisuje točka
. Što opisuje točka  tog trokuta. Točke
tog trokuta. Točke 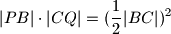
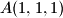 ,
, 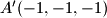 ,
, 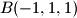 ,
, 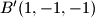 ,
, 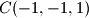 ,
, 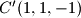 ,
, 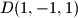 ,
, 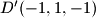 . Točka
. Točka 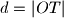 . Označimo s
. Označimo s 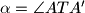 ,
, 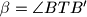 ,
, 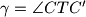 ,
, 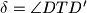 . Dokažite da je
. Dokažite da je