Državno natjecanje 2003 SŠ4 3
prirodni brojevi od
do
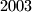
poredani su u niz. na nizu vrsimo ovu operaciju: ako je prvi broj u nizu jednak
, okrenemo poredak prvih
brojeva. dokazati da se nakon konacno uzastopnih primjena ove operacije broj
pojavi na prvom mjestu, nezavisno od pocetnog rasporeda.
%V0
prirodni brojevi od $1$ do $2003$ poredani su u niz. na nizu vrsimo ovu operaciju: ako je prvi broj u nizu jednak $k$, okrenemo poredak prvih $k$ brojeva. dokazati da se nakon konacno uzastopnih primjena ove operacije broj $1$ pojavi na prvom mjestu, nezavisno od pocetnog rasporeda.
Source: Državno natjecanje iz matematike 2003
Školjka 
