Državno natjecanje 2003 SŠ4 4
Dodao/la:
arhiva1. travnja 2012. Dokažite da je
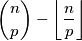
djeljivo s

, za svaki prost broj

i svaki prirodan broj
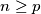
.
%V0
Dokažite da je $${n \choose p} - \left\lfloor \frac{n}{p} \right\rfloor$$ djeljivo s $p$, za svaki prost broj $p$ i svaki prirodan broj $n \geq p$.
Izvor: Državno natjecanje iz matematike 2003