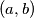
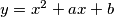
Odredi sve parove cijelih brojeva takve da površina trokuta čiji su vrhovi točke u kojima parabola siječe koordinatne osi iznosi .
%V0
Odredi sve parove $(a, b)$ cijelih brojeva takve da površina trokuta čiji su vrhovi točke u kojima parabola $y = x^2 + ax + b$ siječe koordinatne osi iznosi $3$.
Školjka 
cijelih brojeva takve da površina trokuta čiji su vrhovi točke u kojima parabola 
siječe koordinatne osi iznosi 
.