Državno natjecanje 2004 SŠ4 3
Dodao/la:
arhiva1. travnja 2012. Nizovi realnih brojeva
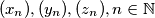
, definirani su formulama
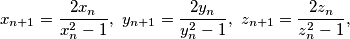
a početni članovi su
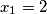
,
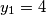
i
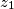
takav da vrijedi
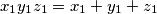
.

Provjerite da su za svaki

zadovoljeni uvjeti:
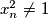
,
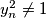
,
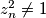
.

Postoji li

takav da je
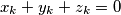
?
%V0
Nizovi realnih brojeva $(x_n), (y_n), (z_n), n \in \mathbb{N}$, definirani su formulama $$x_{n+1}=\frac{2x_n}{x_n^2 - 1}\text{,}\,\,\, y_{n+1}=\frac{2y_n}{y_n^2 - 1}\text{,}\,\,\, z_{n+1}=\frac{2z_n}{z_n^2 - 1}\text{,}$$ a početni članovi su $x_1 = 2$, $y_1 = 4$ i $z_1$ takav da vrijedi $x_1y_1z_1 = x_1 + y_1 + z_1$.
$a)$ Provjerite da su za svaki $n \in \mathbb{N}$ zadovoljeni uvjeti: $x_n^2 \not= 1$, $y_n^2 \not= 1$, $z_n^2 \not= 1$.
$b)$ Postoji li $k \in \mathbb{N}$ takav da je $x_k + y_k + z_k = 0$?
Izvor: Državno natjecanje iz matematike 2004